Types and algorithms for robotic mobile manipulation. More...

Namespaces
namespace	FrameID

Classes
class	ArmModel
	Arm Model class for serial kinematic chains (manipulators). More...

class	ArmModelJointException
	Exception to be thrown when setting joint variable of wrong size. More...

class	ArmModelNotInitializedException
	Exception to be thrown when setting joint variable on a not initialized arm model. More...

class	BaxterLeftArmModel

class	BellShapeParameterException
	FUNCTIONS. More...

class	EulerRPY
	Euler RPY angle representation. More...

class	ExceptionWithHow

class	LabelSyntaxException

class	NewtonEuler
	Implementation of the Newton-Euler equation for rigid-body chains. More...

struct	PlaneParameters
	Using four parameters represention in the form: Ax + By + Cz + D = 0;. More...

struct	RegularizationData
	Regularization parameters and results container. More...

struct	RegularizationParameters

struct	RegularizationResults

class	RobotLink
	Basic element of an ArmModel. More...

class	RobotModel
	Robot Model class, to evaluate either mobile or fixed manipulators total transformation matrices and jacobians. More...

class	RobotModelArmException
	Exception to be thrown in robot model when dealing with the arm model. More...

class	RobotModelWrongControlSizeVectorException
	Exception to be thrown when trying to set a wrong control vector. More...

class	TwoLinksArmModel

class	VehicleModel
	Vehicle Model base class. More...

class	VehicleModelNotInitializedException
	Exception to be thrown when the vehicle model is not initialized. More...

class	WrongFrameException
	Exception to be thrown in robot model when dealing with wrong frame id's. More...

class	YouBotArmModel

class	YouBotVehicleModel

Typedefs
typedef std::pair< std::string, Eigen::TransformationMatrix >	IndexedTMat

Enumerations
enum class	JointType : uint8_t { Fixed , Revolute , Prismatic }
	Used to describe the type of joint. More...

Functions
Eigen::Vector3d	ReducedVersorLemma (const Eigen::Vector3d &v1, const Eigen::Vector3d &v2)
	Compute the misalignment error between two vectors. The result is the vector around which v1 has to rotate to reach v2.

Eigen::Vector3d	VersorLemma (const Eigen::RotationMatrix &r1, const Eigen::RotationMatrix &r2)
	Compute the versor lemma between the two rotation matrices.

Eigen::Vector3d	VersorLemma (const EulerRPY &v1, const EulerRPY &v2)
	Compute the versor lemma between the two rotation matrices.

Eigen::Vector6d	CartesianError (const Eigen::TransformationMatrix &in1, const Eigen::TransformationMatrix &in2)
	Compute the Cartesian error between two transformation matrices.

Eigen::Vector6d	CartesianError (const Eigen::Vector6d &v1, const Eigen::Vector6d &v2)
	Compute the Cartesian error between two transformation matrices.

double	DecreasingBellShapedFunction (double xmin, double xmax, double ymin, double ymax, double x) noexcept(false)
	A decreasing bell shaped (sigmoid) function.

double	IncreasingBellShapedFunction (double xmin, double xmax, double ymin, double ymax, double x) noexcept(false)
	An increasing bell shaped (sigmoid) function.

void	SaturateScalar (double sat, double &value)
	Saturate the scalar to a given maximum value.

void	SaturateVector (const double sat, Eigen::VectorXd &vector)
	Saturate the vector to a given maximum value applying normalization for preserving the vector direction.

void	SaturateVector (const Eigen::VectorXd &upper_limits, const Eigen::VectorXd &lower_limits, Eigen::VectorXd &vect)
	Saturate the vector within the specified limits.

double	DistancePointToPlane (const Eigen::Vector3d &point, const PlaneParameters &planeParams)
	Evaluates the norm of the shortest distance vector among a point and a given plane.

Eigen::Vector3d	ClosestPointOnPlane (const Eigen::Vector3d &point, const PlaneParameters &planeParams)
	Given a point and a plane evaluates the coordinates of the closest point on plane w.r.t the input one.

Eigen::Matrix3d	Vect3ToSkew (const Eigen::Vector3d &t)
	Computes the skew symmetric matrix form for a vector.

Eigen::Matrix6d	RigidBodyMatrix (const Eigen::Vector3d &transl)
	Compute a rigid body matrix.

Eigen::MatrixXd	ChangeJacobianObserver (Eigen::MatrixXd J, Eigen::MatrixXd Jobserver, Eigen::Vector3d CartesianError)
	ChangeJacobianObserver Method implementing change of observer for a cartesian Jacobian. .

template<class MatT >
MatT	GreatestNormElement (const MatT &vect1, const MatT &vect2, const MatT &vect3)
	An utility to find the vector with the greatest norm among three.

template<typename T >
int	sgn (T val)

void	Double2Matrix (double dmat[], int rows, int cols, Eigen::MatrixXd &MatT)

void	Matrix2Double (const Eigen::MatrixXd &MatT, int rows, int cols, double dmat[])

void	Double2Vector (double dmat[], int rows, Eigen::VectorXd &MatT)

void	Vector2Double (const Eigen::VectorXd &MatT, int rows, double dmat[])

void	SetDiagonalFromDouble (Eigen::MatrixXd &MatT, double diag[])

Eigen::MatrixXd	RightJuxtapose (const Eigen::MatrixXd &A, const Eigen::MatrixXd &B)

Eigen::MatrixXd	UnderJuxtapose (const Eigen::MatrixXd &A, const Eigen::MatrixXd &B)

void	RegPinv (const double J, int m, int n, double JPInv, double treshold, double lambda, double prod, int flag)

template<class MatT >
Eigen::Matrix< typename MatT::Scalar, MatT::ColsAtCompileTime, MatT::RowsAtCompileTime >	RegularizedPseudoInverse (const MatT &mat, RegularizationData &regData)
	Computes the SVD-based regularized matrix pseudoinversion (A = USV')

void	SVD_NumericalRecipes (double a, int m, int n, double w, double v, double rv1)

template<class MatT >
void	SVD (const MatT &A, MatT &U, MatT &S, MatT &V)
	Singular Value Decomposition.

double	RaisedCosine (double in, double th, double lambda)

short	MatrixMultiply (const double A, int m, int n, const double B, char k, char p, double *OUT)

void	MatrixTranspose (const double A, int m, int n, double OUT)

double	SmoothTransition (double x, double beta, double xmin, double lambda)

double	SmoothFunction (double x, double beta, double lambda)

Variables
const double	STD_GRAVITY = 9.80665

const std::map< JointType, std::string >	JointType2String

const double	RPY2VectEpsilon = 0.000000001

const unsigned long int	MaxMatrixDim = 1300
	Max matrices dimension.

const double	SVDEpsilon = 0.00000001

Detailed Description

Types and algorithms for robotic mobile manipulation.

The "Robotic Mathematical Library" is a minimal and portable math lib for robotics that relies on Eigen. It includes tools for matrix pseudo inversion and the SVD algorithm. It also provides utility functions for type conversion and data extraction for transformation and rotation matrices, RPY angle representation, rigid body matrices and matrix juxtaposition.

Types:

EulerRPY
(Eigen::RotMatrix, Eigen::TransfMatrix and Eigen::Vector6d have been defined inside the Eigen namespace)

Structs:

PlaneParameters

Strong Enums:

JointType

Classes:

Functions:

Algorithms:
- SVD()
- RegularizedPseudoInverse()
Geometric:
- VersorLemma()
- CartesianError()
- DistancePointToPlane()
- ClosestPointOnPlane()
- GetRigidBodyMatrix()
Utilities:

Typedef Documentation

◆ IndexedTMat

typedef std::pair<std::string, Eigen::TransformationMatrix> rml::IndexedTMat

Enumeration Type Documentation

◆ JointType

enum class rml::JointType : uint8_t

strong

Used to describe the type of joint.

Enumerator
Fixed
Revolute
Prismatic

Function Documentation

◆ CartesianError() [1/2]

Eigen::Vector6d rml::CartesianError	(	const Eigen::TransformationMatrix &	in1,
		const Eigen::TransformationMatrix &	in2
	)

Compute the Cartesian error between two transformation matrices.

The method computes the misalignment error and the position error between two transformation matrices It uses the VersorLemma to compute the misalignment, and a simple difference to compute the linear distance The result is the error that brings in1 towards in2

Parameters

[in]	in1	the initial transformation matrix
[in]	in2	the goal transformation matrix

Returns: the Vect6 representing the axis around which in2 should rotate to reach in1 and the linear distance

Note: the two transformation matrix should have a common base frame, i.e. CartesianError(wTt, wTg) brings the tool frame <t> towards a goal frame <g>, and returns the error projected on frame <w>

◆ CartesianError() [2/2]

Eigen::Vector6d rml::CartesianError	(	const Eigen::Vector6d &	v1,
		const Eigen::Vector6d &	v2
	)

Compute the Cartesian error between two transformation matrices.

The method computes the misalignment error and the position error between two transformation matrices expressed as their 6 parameters representation The method assumes that the two Vect6 are a 6 parameter representation of the type v = [yaw pitch roll x y z] leading to the following rotational part R = Rz(yaw) * Ry(pitch) * Rx(roll) It uses the VersorLemma to compute the misalignment, and a simple difference to compute the linear distance The result is the error that brings in1 towards in2

Parameters

[in]	v1	the initial transformation matrix expressed as its 6 parameter representation
[in]	v2	the goal transformation matrix expressed as its 6 parameter representation

Returns: the Vect6 representing the axis around which in2 should rotate to reach in1 and the linear distance

Note: the two vector should represent transformation matrix computed w.r.t a common frame, i.e. v1 = wTt, v2 = wTg then CartesianError(v1, v2) brings the tool frame <t> towards a goal frame <g>, and returns the error projected on frame <w>

◆ ChangeJacobianObserver()

Eigen::MatrixXd rml::ChangeJacobianObserver	(	Eigen::MatrixXd	J,
		Eigen::MatrixXd	Jobserver,
		Eigen::Vector3d	CartesianError
	)

ChangeJacobianObserver Method implementing change of observer for a cartesian Jacobian.
.

$J^{v}_{error}=J^{o}_{error}-S_{e/o}J^{o}_{v}$

Parameters

J	error jacobian wrt to the inertial frame
Jobserver	jacobian of the observer wrt to the inertial frame
CartesianError	error

Returns: Jacobian of the error observed by the input observer

◆ ClosestPointOnPlane()

Eigen::Vector3d rml::ClosestPointOnPlane	(	const Eigen::Vector3d &	point,
		const PlaneParameters &	planeParams
	)

Given a point and a plane evaluates the coordinates of the closest point on plane w.r.t the input one.

Parameters

[in]	point	The point from where calculate the distance
[in]	planeParams	The target plane

Returns: The 3d coordinates of the closest point laying on the plane

◆ DecreasingBellShapedFunction()

double rml::DecreasingBellShapedFunction	(	double	xmin,
		double	xmax,
		double	ymin,
		double	ymax,
		double	x
	)

A decreasing bell shaped (sigmoid) function.

The output of this function has a smooth behavior, starting from the value (xmin, ymax) to (xmax, ymin) For $x < x_{min}, y = y_{max}$
For $x > x_{max}, y = y_{min}$

Parameters

[in]	xmin	the lower extreme value where the transition begins
[in]	xmax	the higher extreme value where the transition stops
[in]	ymin	the lowest value of the function
[in]	ymax	the highest value of the function
[in]	x	the value where the function is evaluated

Returns: the value of the function

◆ DistancePointToPlane()

double rml::DistancePointToPlane	(	const Eigen::Vector3d &	point,
		const PlaneParameters &	planeParams
	)

Evaluates the norm of the shortest distance vector among a point and a given plane.

Parameters

[in]	point	The point from where calculate the distance
[in]	planeParams	The target plane

Returns: The distance norm

◆ Double2Matrix()

void rml::Double2Matrix	(	double	dmat[],
		int	rows,
		int	cols,
		Eigen::MatrixXd &	MatT
	)

inline

◆ Double2Vector()

void rml::Double2Vector	(	double	dmat[],
		int	rows,
		Eigen::VectorXd &	MatT
	)

inline

◆ GreatestNormElement()

template<class MatT >

MatT rml::GreatestNormElement	(	const MatT &	vect1,
		const MatT &	vect2,
		const MatT &	vect3
	)

An utility to find the vector with the greatest norm among three.

Parameters

vect1
vect2
vect3

Returns: The vector with the greatest norm among the three

◆ IncreasingBellShapedFunction()

double rml::IncreasingBellShapedFunction	(	double	xmin,
		double	xmax,
		double	ymin,
		double	ymax,
		double	x
	)

An increasing bell shaped (sigmoid) function.

The output of this function has a smooth behavior, starting from the value (xmin, ymin) to (xmax, ymax)
For $x < x_{min}, y = y_{min}$
For $x > x_{max}, y = y_{max}$

Parameters

[in]	xmin	the lower extreme value where the transition begins
[in]	xmax	the higher extreme value where the transition stops
[in]	ymin	the lowest value of the function
[in]	ymax	the highest value of the function
[in]	x	the value where the function is evaluated

Returns: the value of the function

◆ Matrix2Double()

void rml::Matrix2Double	(	const Eigen::MatrixXd &	MatT,
		int	rows,
		int	cols,
		double	dmat[]
	)

inline

◆ MatrixMultiply()

short rml::MatrixMultiply	(	const double *	A,
		int	m,
		int	n,
		const double *	B,
		char	k,
		char	p,
		double *	OUT
	)

◆ MatrixTranspose()

void rml::MatrixTranspose	(	const double *	A,
		int	m,
		int	n,
		double *	OUT
	)

◆ RaisedCosine()

double rml::RaisedCosine	(	double	in,
		double	th,
		double	lambda
	)

◆ ReducedVersorLemma()

Eigen::Vector3d rml::ReducedVersorLemma	(	const Eigen::Vector3d &	v1,
		const Eigen::Vector3d &	v2
	)

Compute the misalignment error between two vectors. The result is the vector around which v1 has to rotate to reach v2.

Parameters

[in]	v1	first orientation vector
[in]	v2	second orientation vector

Returns: the axis around which v1 has to rotate to reach v2

◆ RegPinv()

void rml::RegPinv	(	const double *	J,
		int	m,
		int	n,
		double *	JPInv,
		double	treshold,
		double	lambda,
		double *	prod,
		int *	flag
	)

◆ RegularizedPseudoInverse()

template<class MatT >

Eigen::Matrix< typename MatT::Scalar, MatT::ColsAtCompileTime, MatT::RowsAtCompileTime > rml::RegularizedPseudoInverse	(	const MatT &	mat,
		RegularizationData &	regData
	)

Computes the SVD-based regularized matrix pseudoinversion (A = U*S*V')

The regularization, being $\sigma_i$ the i-th singular value, is performed using following formula:
$\sigma_i = \sigma_i / ({\sigma_i}^2 + Reg)$ , where, using the raised cosine
$Reg = \left\{ \begin{array}{ll} lambda/2 * (1 + cos((\sigma_i / thresh) * \pi)) & \mbox{if $0 \leq \sigma_i \leq th$}\\ 0 & \mbox{elsewhere}. \end{array} \right.$

Parameters

mat	The matrix to be inverted
regData	The regularization parameters and results struct

Returns: The pseudo-inverse matrix of mat

◆ RightJuxtapose()

Eigen::MatrixXd rml::RightJuxtapose	(	const Eigen::MatrixXd &	A,
		const Eigen::MatrixXd &	B
	)

inline

◆ RigidBodyMatrix()

Eigen::Matrix6d rml::RigidBodyMatrix ( const Eigen::Vector3d & transl )

Compute a rigid body matrix.

This method assumes that the three values stored in the Vect3 correspond to a translation r between two frames Then it computes the rigid body transformation matrix defined as

$\left| \begin{array}{c} \omega \\ v \end{array} \right| = \left| \begin{array}{cc} I_{3 \times 3} & 0_{3 \times 3} \\ -r\wedge & I_{3 \times 3} \\ \end{array} \right| \left| \begin{array}{c} \omega \\ v \end{array} \right|$

Returns: the rigid body matrix

◆ SaturateScalar()

void rml::SaturateScalar	(	double	sat,
		double &	value
	)

Saturate the scalar to a given maximum value.

Parameters

[in]	sat	the value of the saturation
[in,out]	value	the value which is saturated to the maximum value

◆ SaturateVector() [1/2]

void rml::SaturateVector	(	const double	sat,
		Eigen::VectorXd &	vector
	)

Saturate the vector to a given maximum value applying normalization for preserving the vector direction.

Parameters

[in]	sat	the value of the saturation
[in,out]	vector	the vector which is saturated to the maximum value

◆ SaturateVector() [2/2]

void rml::SaturateVector	(	const Eigen::VectorXd &	upper_limits,
		const Eigen::VectorXd &	lower_limits,
		Eigen::VectorXd &	vect
	)

Saturate the vector within the specified limits.

This function ensures that all components of a given vector remain within the bounds defined by the provided upper and lower limits. If any component of the vector exceeds its corresponding upper limit or falls below its lower limit, the entire vector is scaled proportionally to keep all components within the valid range.

The scaling process ensures that the direction of the vector is preserved while bringing all components within bounds. The scaling factor is calculated based on the strictest limit violation across all components.

Parameters

[in]	upper_limits	The upper limits for each component of the vector. This must be the same size as the input vector.
[in]	lower_limits	The lower limits for each component of the vector. This must be the same size as the input vector.
[in,out]	vect	The vector to be saturated. This vector is updated in place to ensure all its components lie within the specified bounds.

Note: If the size of the upper_limits or lower_limits vectors does not match the size of the input vect, the function will throw a std::invalid_argument exception.

Exceptions

std::invalid_argument If the size of the upper_limits or lower_limits does not match the size of vect.

◆ SetDiagonalFromDouble()

void rml::SetDiagonalFromDouble	(	Eigen::MatrixXd &	MatT,
		double	diag[]
	)

inline

◆ sgn()

template<typename T >

int rml::sgn ( T val )

◆ SmoothFunction()

double rml::SmoothFunction	(	double	x,
		double	beta,
		double	lambda
	)

◆ SmoothTransition()

double rml::SmoothTransition	(	double	x,
		double	beta,
		double	xmin,
		double	lambda
	)

◆ SVD()

template<class MatT >

void rml::SVD	(	const MatT &	A,
		MatT &	U,
		MatT &	S,
		MatT &	V
	)

Singular Value Decomposition.

The methods computes the singular value decomposition of the given matrix A, defined as A = USV'. If A is of size m x n, then U is m x m, S is m x n and V is n x n

Parameters

[in]	A	the matrix to be decomposed
[out]	U	the m x m rotation matrix
[out]	S	the m x n singular values matrix
[out]	V	the n x n rotation matrix

◆ SVD_NumericalRecipes()

void rml::SVD_NumericalRecipes	(	double *	a,
		int	m,
		int	n,
		double *	w,
		double *	v,
		double *	rv1
	)

◆ UnderJuxtapose()

Eigen::MatrixXd rml::UnderJuxtapose	(	const Eigen::MatrixXd &	A,
		const Eigen::MatrixXd &	B
	)

inline

◆ Vect3ToSkew()

Eigen::Matrix3d rml::Vect3ToSkew ( const Eigen::Vector3d & t )

Computes the skew symmetric matrix form for a vector.

The output is the following:
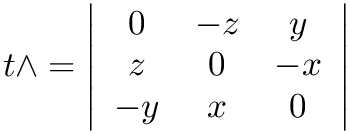
$t\wedge = \left| \begin{array}{ccc} 0 & -z & y \\ z & 0 & -x \\ -y & x & 0 \end{array} \right|$

Parameters

t	input vector

Returns: the skew symmetric matrix

◆ Vector2Double()

void rml::Vector2Double	(	const Eigen::VectorXd &	MatT,
		int	rows,
		double	dmat[]
	)

inline

◆ VersorLemma() [1/2]

Eigen::Vector3d rml::VersorLemma	(	const Eigen::RotationMatrix &	r1,
		const Eigen::RotationMatrix &	r2
	)

Compute the versor lemma between the two rotation matrices.

Computes the misalignment vector between the two frames, represented by the two rotation matrices The vector is the axis around which the first frame should rotate in order to become equal to the second (angle-axis representation)

Parameters

[in]	r1	the first rotation matrix
[in]	r2	the second rotation matrix

Returns: the Vect3 representing the axis around which r1 should rotate to reach r2, where its modulus is the angle

Note: the two rotation matrix should be w.r.t a common frame, i.e. r1 = cRa, r2 = cRb then the versor lemma gives the rotation vector that brings frame <a> over frame <b> projected on <c>

◆ VersorLemma() [2/2]

Eigen::Vector3d rml::VersorLemma	(	const EulerRPY &	v1,
		const EulerRPY &	v2
	)

Compute the versor lemma between the two rotation matrices.

Computes the misalignment vector between the two frames, represented by the two rotation matrices expressed as their RPY representation In particular, both v1 and v2 are assumed to be in the form: [yaw -pitch roll] giving the following matrix R = Rz(yaw) * Ry(pitch) * Rx(roll) The vector is the axis around which the first frame should rotate in order to become equal to the second (angle-axis representation).

Parameters

[in]	v1	the RPY representation of the first rotation matrix
[in]	v2	the RPY representation of the second rotation matrix

Returns: the Vect3 representing the axis around which v1 should rotate to reach v2, where its modulus is the angle

Note: the two vector should represent rotation matrices computed w.r.t a common frame, i.e. r1 = cRa, r2 = cRb then the versor lemma gives the rotation vector that brings frame <a> over frame <b> projected on <c>

Variable Documentation

◆ JointType2String

const std::map<JointType, std::string> rml::JointType2String

Initial value:

= {
    { JointType::Fixed, "Fixed" },
    { JointType::Revolute, "Revolute" },
    { JointType::Prismatic, "Prismatic" }
}

◆ MaxMatrixDim

const unsigned long int rml::MaxMatrixDim = 1300

Max matrices dimension.

◆ RPY2VectEpsilon

const double rml::RPY2VectEpsilon = 0.000000001

◆ STD_GRAVITY

const double rml::STD_GRAVITY = 9.80665

◆ SVDEpsilon

const double rml::SVDEpsilon = 0.00000001

Namespaces

Classes

Typedefs

Enumerations

Functions

Variables

Detailed Description

Typedef Documentation

◆ IndexedTMat

Enumeration Type Documentation

◆ JointType

Function Documentation

◆ CartesianError() [1/2]

◆ CartesianError() [2/2]

◆ ChangeJacobianObserver()

◆ ClosestPointOnPlane()

◆ DecreasingBellShapedFunction()

◆ DistancePointToPlane()

◆ Double2Matrix()

◆ Double2Vector()

◆ GreatestNormElement()

◆ IncreasingBellShapedFunction()

◆ Matrix2Double()

◆ MatrixMultiply()

◆ MatrixTranspose()

◆ RaisedCosine()

◆ ReducedVersorLemma()

◆ RegPinv()

◆ RegularizedPseudoInverse()

◆ RightJuxtapose()

◆ RigidBodyMatrix()

◆ SaturateScalar()

◆ SaturateVector() [1/2]

◆ SaturateVector() [2/2]

◆ SetDiagonalFromDouble()

◆ sgn()

◆ SmoothFunction()

◆ SmoothTransition()

◆ SVD()

◆ SVD_NumericalRecipes()

◆ UnderJuxtapose()

◆ Vect3ToSkew()

◆ Vector2Double()

◆ VersorLemma() [1/2]

◆ VersorLemma() [2/2]

Variable Documentation

◆ JointType2String

◆ MaxMatrixDim

◆ RPY2VectEpsilon

◆ STD_GRAVITY

◆ SVDEpsilon